Curvature-Directed Rendering

Key Features

• Principal direction/curvature for SDFs
• Parallel Poisson disk sampling across SDF surfaces
• Procedural geometry generation with compute shaders

Description

I developed this rendering technique while working on a VR visualization system for radiation treatment planning teams at the Mayo Clinic.

A key challenge in the development of this visualization system was determining how to render both the radiation dosage volume and the anatomical context together in one view without them occluding each other.

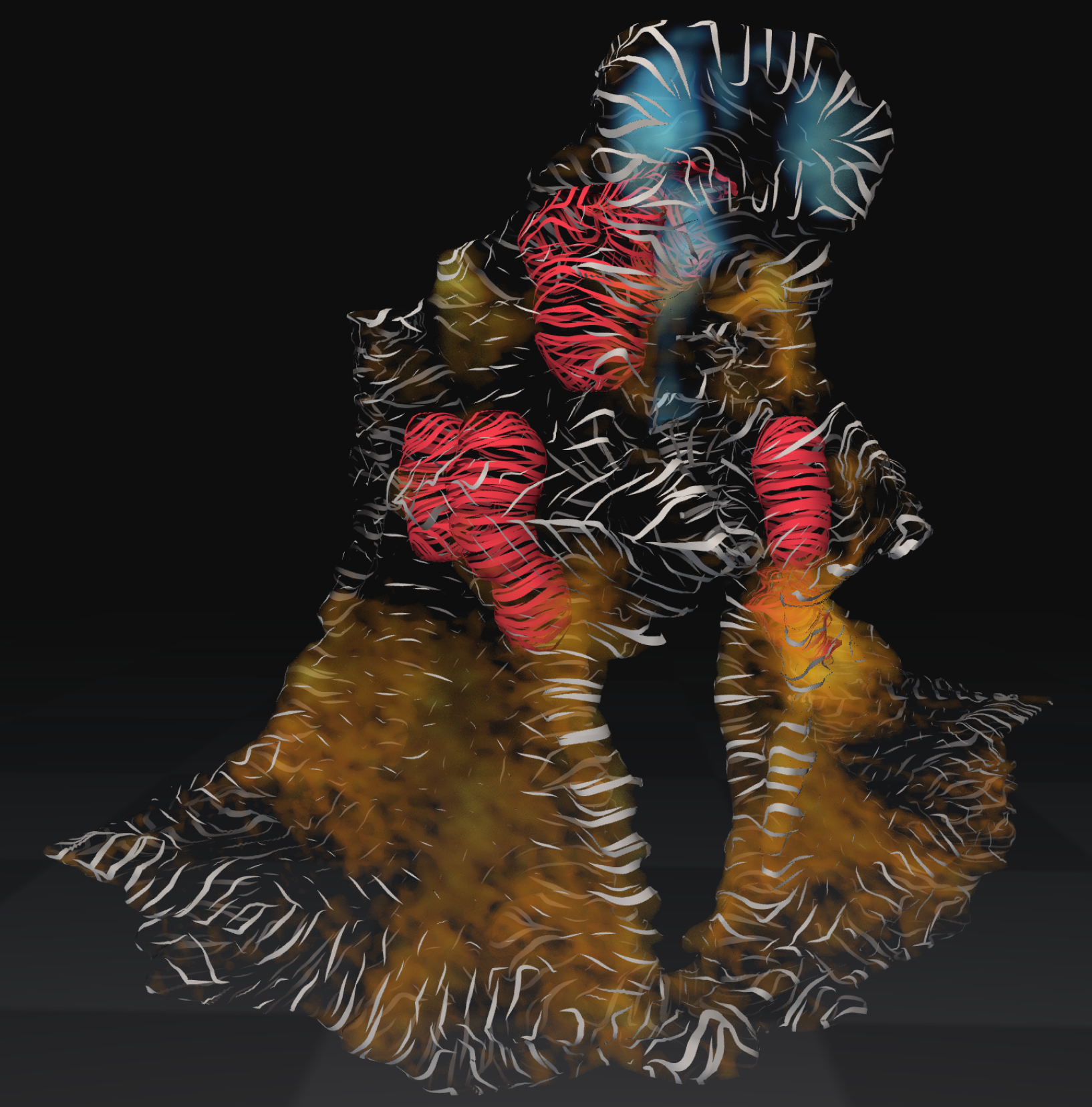
Building off of past research on the topic which found that the most perceptually optimal way to render such surface-inside-a-surface interactions involves the usage of curvature-directed lines, I created a entirely GPU-based rendering pipeline that generates curvature-directed lines for SDFs procedurally using compute shaders.

Discussion

History

When visualizing 3D data it is often necessary to make complex spatial judgments about how multiple surfaces/volumes fit within one another or overlap. While using transparency is a tempting approach to solving this problem, in reality it is less than ideal. This is because intuiting the shape of surfaces becomes increasingly difficult as lighting queues diminish with increased transparency, not to mention the issue of alpha sorting for overlapping objects.

Instead, research has shown that the most perceptually optimal rendering techniques for facilitating surface-inside-a-surface spatial judgments make use of curvature-directed lines to communicate the shape of one or more of the surfaces. V. Interrante is a pioneer in this field, and her research laid the groundwork for the development of the technique demonstrated here.

More specifically, the rendering technique demonstrated here is modernization of Interrante's work, where instead of relying on curvature-directed textures generated offline, every step of the process is now run entirely on the GPU, transforming this into interactive rendering technique run in real-time.

My Implementation

To generate curvature-directed lines for an SDF in real-time, each of the following steps is run on the GPU via compute shaders:

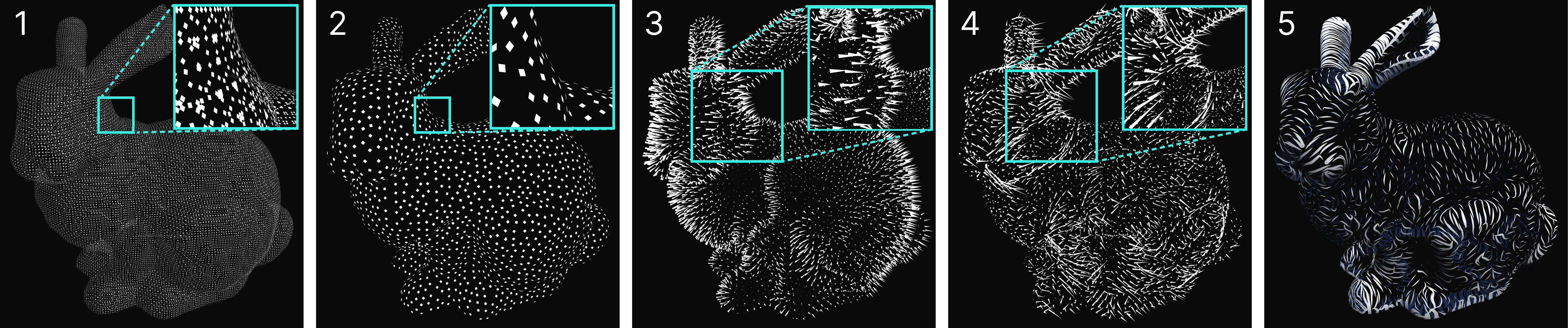
1. First, a set of arbitrary points are densely sampled along the surface of the SDF. These points are sampled in the same way that surface points are sampled in the Marching Cubes algorithm, wherein the voxel positions of neighboring voxel pairs in which one voxel sits inside the surface while the other voxel sits outside the surface are interpolated to generate points that lie along the isosoruface of the SDF.
2. Second, Poisson disk sampling is used to transform the dense initial point set into a uniform distribution, in which no two points are closer to one another than a specified distance. This is done to improve the perceptual effectiveness of the technique.
3. Third, the gradient of the SDF is calculated at every voxel using central differences. The gradient is used in the next step to derive principal curvature, as well as in the last step to give the lines proper normals and ensure they stay fixed to the surface of the SDF.
4. Fourth, the first principal direction along with the first principal curvature are computed for each voxel in the SDF. This is done by using the gradients calculated in the previous step to generate a 2D orthonormal basis in the tangent plane at each voxel from which a 2x2 Hessian matrix can be derived. Diagonalizing this matrix, also known as the second fundamental form, gives us its eigenvectors and eigenvalues, which are equivalent to the principal directions and curvatures.
5. Finally, a compute shader generates curvature-directed lines outward in both directions from each starting point using the fourth order Runge-Kutta method to integrate a path along the first principal direction. The principal direction from the previous step is used to maintain heading, and the traced point is projected onto the surface after each step using the gradient of the SDF and the distance to ensure the lines remain fixed to the surface of the SDF. Line length and width is determined by remapping the first principal curvature value of the starting point using min and max values calculated atomically in a compute shader just before this step. Since the triangles for the lines are generated directly on the GPU, they can immediately be rendered by a custom shader.

Challenges

Line Integral Convolution

Interrante's original work on illustrating surface shape with curvature utilizes Line Integral Convolution (LIC) to generate a curvature-directed stroke texture that can be applied to the surface of the object. I initially took this approach as well, but found that the results it generated suffered from three major issues.

Firstly, without the use of multiple LIC textures at varying scales (which consume valuable VRAM and increase the computational workload) it is not possible to modify the width of the strokes——especially not at a per-stroke level——which is necessary to maximize the perceptual effectiveness of the technique. Secondly, to achieve a high density of curvature-directed lines (similar what is demonstrated in many of the images throughout this page) an absurdly high-resolution 3D LIC texture would need to be used (we're talking gigabytes), further tanking memory usage and general performance. The final issue was that LIC could not guarantee that strokes would remain fixed to the surface of the object, since it was tracing principal curvature directions throughout the entire volume of the SDF. This created aliasing artifacts causing the rendered lines to look "moth-eaten," a drawback described in the original paper.

With the drawbacks of the LIC approach at hand, I decided to generate the curvature-directed lines with triangles instead, as this would grant me greater control over their length, width and general appearance. Combatting the issue of lines not remaining fixed to the object surface was trivial with this approach as well, as the normal and distance information already provided by the SDF could be used to project the line back onto the surface at each step in line generation.

Not only did this approach solve all of the major issues with the LIC approach, but it also ran considerably faster, and generated geometry on the GPU which could be instantly accessed by shaders for rendering.

Curvature Sampling Distance

The sampling distance chosen when computing the Hessian matrix from which to derive curvature is paramount to the perceptual accuracy of the final output: too large of a distance and the surface is likely to be considered uniformly curved, too low of a distance and the slightest of changes in the gradient from voxel-to-voxel will create artifacts in the final image.

To compensate for this reality, I've found that it's possible to pre-compute an “ideal” sampling distance for a given SDF by calculating the coefficient of variation in first principal curvature values for a series of increasing sampling distances and selecting the distance for which first principal curvatures have a coefficient of variation closest to one. Good default values for all other rendering parameters, such as line length, line width, and line spacing, can then be calculated as scalar multiples of said sampling distance.

Demo

The main benefit of being an entirely GPU-based technique is that rendering parameters can be adjusted interactively in real-time:

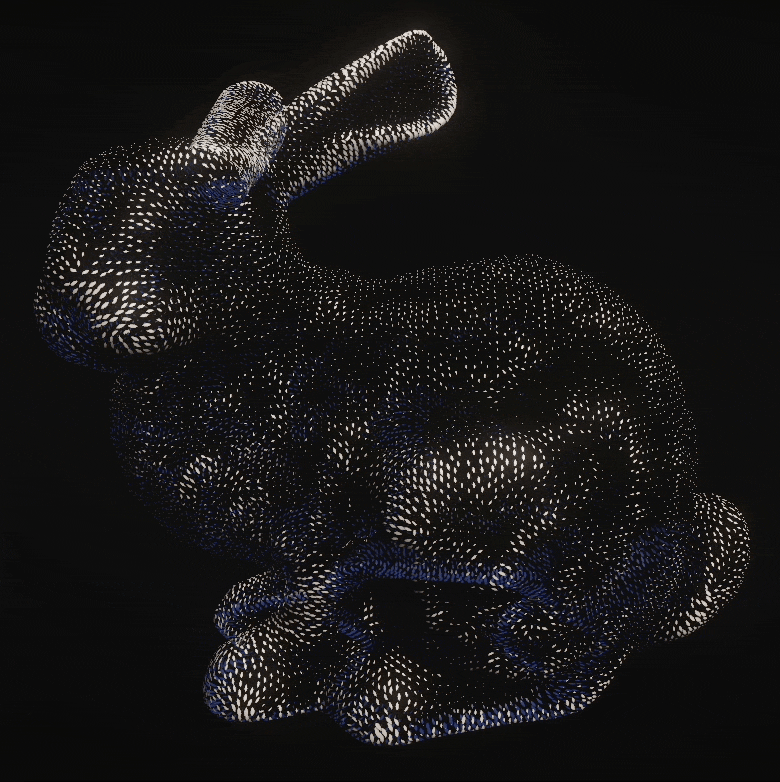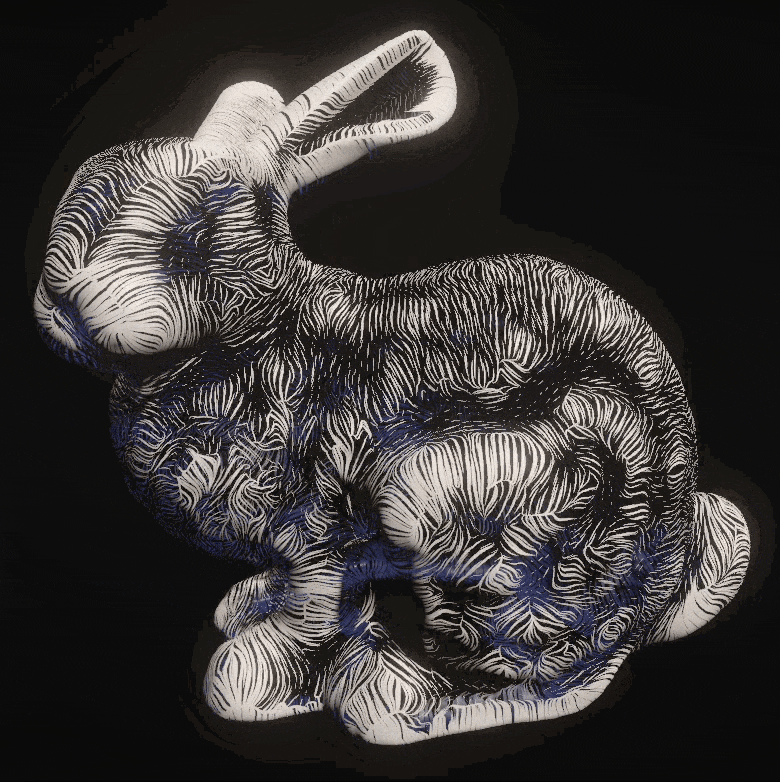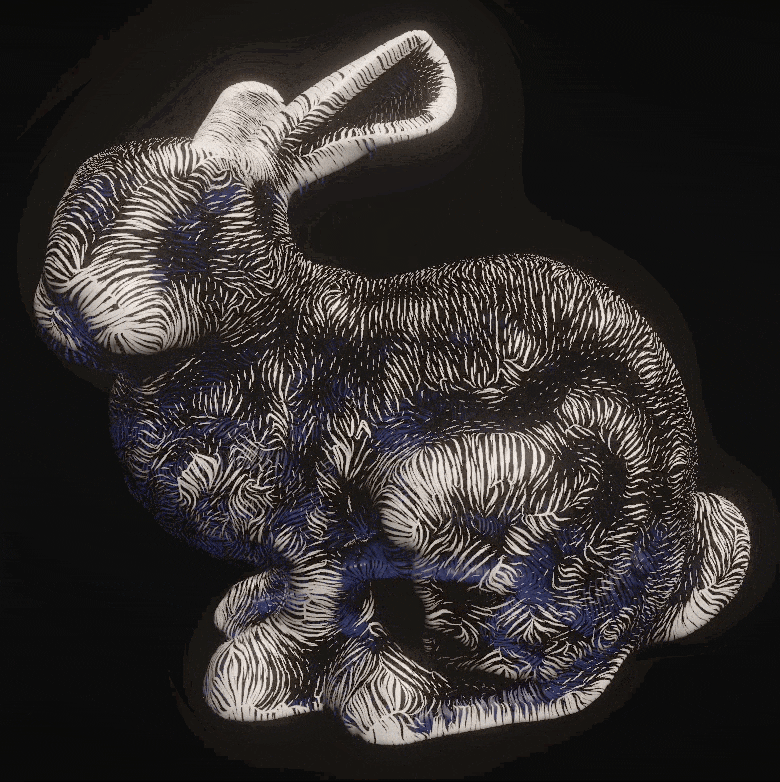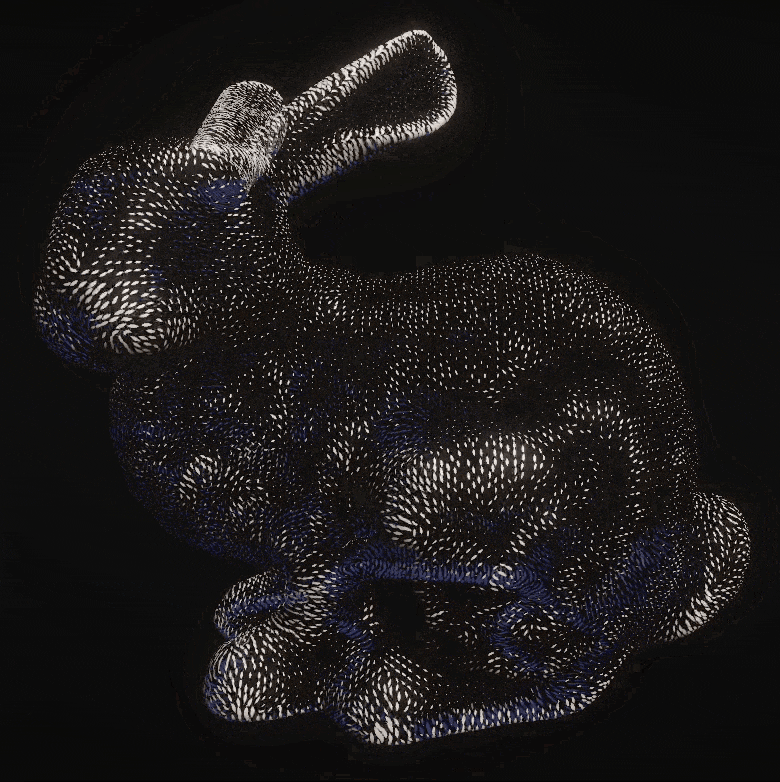
The perceptual effectiveness of the technique is maximized by tapering the curvature-directed lines, scaling their length and width by first principal curvature, and using poisson disk sampling, as demonstrated below:

Credit

The technique presented here is a modernization of Victoria Interrante's excellent work on illustrating surface shape with curvature:

• Illustrating surface shape in volume data via principal direction-driven 3D line integral convolution
• Illustrating transparent surfaces with curvature-directed strokes
• Conveying the 3D shape of smoothly curving transparent surfaces via texture

The GPU poisson disk sampling algorithm used is an interpretation of the technique described in the following paper:

• Parallel Poisson disk sampling with spectrum analysis on surfaces

Tools Used

Languages: C#, HLSL

Software: Unity, Git, mesh-to-sdf (for generating an SDF of the Stanford Bunny)